IONOSPHERE
General Information on the Ionosphere
- The ionosphere is that region of the atmosphere surrounding the earth that is ionized primarily by the solar radiation.
- During the day the ionized layers exist between 90 to 1000 km above the earth’s surface.
- The electron density is of order 1010 to 1012 electrons per meter cube.
- There are primarily three layers in which electron density peaks up (D, E and F layers).
- During day time the F layer splits into two layers F1 and F2.
- D layer disappears at night.
- Ionized layers causes radio waves, less than 40 - 50 MHz, to bend and refract back to earth.
- The electron concentrations vary from seconds to years having various periodicities like hourly, monthly, seasonal and yearly, sunspot cycles.
- Digital high speed data communications over ionosphere is still under development due to high variability of the ionosphere with respect to time, space and frequency.
- On earth there are basically three different regions: high latitude (polar), midlatitude and equatorial.
- Least problematic and most stable is the midlatitude ionosphere.
- Communication is usually performed over E and F layers. D layer introduces attenuation and absorption.
• D layer
This layer contains some free electrons and ions, but also many more normal (or neutral meaning uncharged) molecules and atoms. When radiation interacts with an electron it cause the electron to move. If the electron runs into a neutral molecule or atom, it is absorbed and so is the energy from the radiation. Therefore the primary effect of this layer is to absorb radiation. This is bad for transmissions because when the radiation is absorbed, the signal is lost. The lower the frequency of transmission the more the electron moves and the more likely it is to be absorbed. Therefore the lower the frequency the more the D layer absorbs the transmission energy.
• E layer
This central part of this layer represent contains another peak or maximum value in electron density. However there are fewer electrons in the E layer compared to the F layer and therefore it is not usually as important for bending of HF radiation as the F layer. Some lower HF frequencies, particularly during the day, will be reflected by this layer, which, because it is lower then the F layer, may result in reduced range. This layer is highly variable in space and time. Sometimes disturbances will cause abnormal reflections in parts of the E layer. When this occurs a Sporadic E layer is said to be present.
• F layer
The F layer is the highest significant layer in the ionosphere and the central part has has the greatest electron density in the earth’s atmosphere. This is the main region where HF radiation from below is bent back down. We use the term ”reflection” in the table because the bending is like a reflection. Technically, this bending process is called refraction, but we can think of it as a reflection from the F layer. During the day the F layer separates into two layers, called F1 and F2. The F2 is the stronger and more important layer.
- In an ionized gas, only the motion of electrons is important under the action of a high-frequency electric field, since the ions are more than 1800 times heavier.
- The equation of motion for a single electron of mass m, charge -e, with velocity v, acting upon by and electric field is
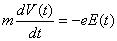 (1) (1)
• In phasor form
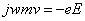 (2) (2)
• For N electrons per unit volume, the induced current in the ionized gas will be
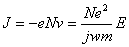 (3) (3)
• From Maxwell’s equations we have
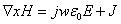 (4) (4) 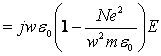 (5) (5)
from which we find the relative dielectric constant of an ionized gas (plasma) as
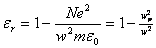 (6) (6)
where the plasma frequency 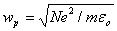 . .
- Here the relative dielectric constant is a function of frequency, thus the medium is called frequency dispersive (or temporally dispersive). When
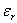 is a function of frequency, the refractive index, n, is also a function of frequency. is a function of frequency, the refractive index, n, is also a function of frequency.
- At lower altitudes the electrons suffer a relatively large number of collisions with the neutral molecules and ions.
- For this case, conservation of momentum requires a collisional damping force -
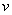 mv to be added to the force equation. mv to be added to the force equation.
- When the collision term is added the relative dielectric constant is complex and is giving in the form
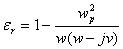 (7) (7)
For 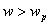 , , 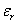 <1. When <1. When 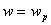 , ,  = 0. When = 0. When 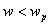 , , 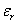 < 0. < 0.
- For plane waves propagating in an ionized gas, propagation constant is
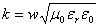 . .
- When
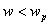 , , 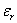 < 0 and k is pure imaginary, plane wave is evanescent and decay exponentially with distance. < 0 and k is pure imaginary, plane wave is evanescent and decay exponentially with distance.
- Thus a plane wave which is normally incident on an ionized gas (in which the electron density increases with height), will propagate at a distance until the wave reaches the height where electron density is sufficient to make
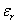 = 0. = 0.
- Then the propagation ceases and the wave is reflected back to earth. For oblique incidence, the ray will be bent and reflected at the height where
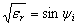
- Critical frequency for a given layer is the highest frequency that will be returned down to earth by that layer after having been beamed straight up at it.
- Skip distance is the shortest distance from the transmitter at which a sky wave of fixed frequency will be returned to earth.
- Refraction in the Ionosphere
- When a radio wave is transmitted into an ionized layer, refraction, or bending of the wave, occurs. Refraction is caused by an abrupt change in the velocity of the upper part of a radio wave as it strikes or enters a new medium. The amount of refraction that occurs depends on three main factors:
- the density of ionization of the layer,
- the frequency of the radio wave, and
- the angle at which the wave enters the layer.
• There is an upper limit on frequency which will result in the wave being returned to
earth. The required relationship between the electron density and the frequency and the
angle of incidence is
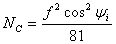
• For a given value of Nmax, for the normal incidence, the frequency that makes 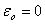 is is
called the critical frequency and is given by
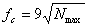 (9) (9)
• For the oblique incidence, from previous equation for Nmax,
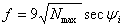 (10) (10)
- This value of
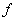 is called the maximum usable frequency (MUF) when is called the maximum usable frequency (MUF) when 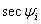 has its maximum value. The MUF usually does not exceed 40 MHz. has its maximum value. The MUF usually does not exceed 40 MHz.
- During periods of low solar activity the upper frequency limit is 25 to 30 MHz.
- If the incident and returned rays are extrapolated to a vertex they meet at a height h’ called the virtual height of the ionospheric layer.
- This is the apparent height of reflection.
- The virtual heights are important in determining the maximum value of the angle of incidence ^ and the maximum skip distance.
- The horizontal skip distance is given by
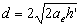 . The corresponding maximum value of . The corresponding maximum value of 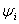 is given by is given by
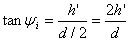 (11) (11)
- Propagation in Anisotropic Cold Plasma
- A free electron will rotate or move in a circular orbit under the influence of a steady magnetic field. The cyclotron frequency is the angular frequency which the free electron rotates under the influence of a steady magnetic field. This rotation has to be included into the force equation. The anisotropicity of the plasma is due to this cyclotron frequency. Cold plasma means thermo-dynamic effects acting on the electron are neglected.
- The earth’s magnetic field is quite important on ionospheric propagation especially for frequencies below 5 MHz.
- The earth’s magnetic field causes the ionospheric medium to become anisotropic and the effective relative dielectric constant must be represented by a matrix or dyadic.
- There are two distinct propagation modes ordinary and extraordinary.
- An incident plane wave entering the ionosphere will split into ordinary and extraordinary modes and when these modes reemerge from the ionosphere they recombine into a single plane wave again.
- However, the plane of polarization will usually have changed (Faraday Rotation). This effect causes polarization mismatch at the receiving antenna.
- The equation of motion for a single electron of mass m, charge -e, with velocity v, acting upon by and electric field is
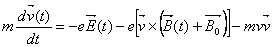 (12) (12)
• In phasor form
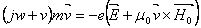 (13) (13)
The value of the magnetic field of the wave is quite small compared to the dc magnetic field of the earth. So it is neglected.
• Rewrite the above equation using the plasma frequency
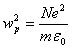 (14) (14)
and cyclotron frequency
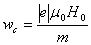 (15) (15)
• The earth’s magnetic field can be expressed as
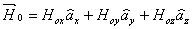 (16) (16)
The polarization vector P is given by
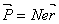 (17) (17)
- Manipulate the above force equation to obtain
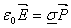 (18) (18)
where
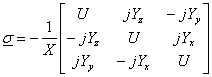 (19) (19)
where
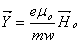 (20) (20)
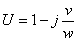 (21) (21)
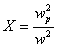 (22) (22)
Invert the matrix to obtain susceptibility
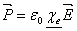 (23) (23)
where
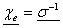 (24) (24)
and
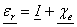 (25) (25)
where 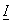 is the identity matrix is the identity matrix
• The wave equation for the electric field is obtained
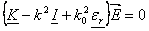 (26) (26)
Where
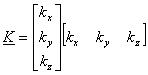 (27) (27)
Non zero solutions for 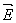 are obtained for determinant zero: are obtained for determinant zero:
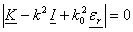 (28) (28)
The solution gives the propagation constant k.
- According to the orientation of the electric field with respect to the earth’s magnetic field (parallel or perpendicular), the wave equation can be solved.
- For each case, the wave equation will lead to two separate propagation constants: ordinary and extraordinary modes. So, the wave will split into two paths (multipath propagation) with different propagation constants, different polarization, different amplitudes and phase shifts and time delays.
- When these modes reemerge from the ionosphere, they will recombine into a single plane wave.
- Due to different phase shifts and polarization rotations of the modes, the two signals can interfere constructively or destructively, a phenomenon known as fading.
- Since the characteristics of ionosphere varies with time, the channel is time varying.
- The propagation path has different dielectric constants functions of space coordinates, so the medium is inhomogeneous.
- The dielectric constant and refractive index are functions of time derivative (or frequency) so the channel is frequency dispersive.
- Dispersion is the distortion of the signal due to propagation constant.
- In the presence of DC Magnetic field, VLF waves can enter the ionosphere and this is the main mechanism of whistler mode. The whistler is a form of radio noise in the audio-frequency range characterized by a whistler tone.
- Faraday Rotation
- When a wave is propagating through an anisotropic medium in the direction of the dc magnetic field, two circularly polarized waves propagate with different propagation constants.
- As a result, if these two circularly polarized waves are properly combined so as to produce a linearly polarized wave at one point, then as the wave propagates, the plane of polarization rotates and the angle of rotation is proportional to the distance travelled. This is called the Faraday Rotation.
- The linearly polarized wave propagates with the propagation constant
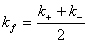 (29) (29)
where k+ is the propagation constant of the ordinary wave and 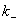 is the propagation constant of the extraordinary wave. is the propagation constant of the extraordinary wave.
• The plane of polarization rotates with the angle
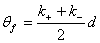 (30) (30)
where d is the distance traveled.
|